本文最后更新于 243 天前,其中的信息可能已经有所发展或是发生改变。
530.二叉搜索树的最小绝对差
思路
把遍历到的节点都加入vec中,在互减得出答案。
题解
递归法
好久没写,手生了,第一次写成前序遍历了,没有利用到二叉搜索树的特性(中序遍历时是从小到大的)
class Solution {
private:
std::vector<int> vec;
void traversal(TreeNode *node) {
vec.push_back(node->val);
if (node->left)
traversal(node->left);
else
return;
if (node->right)
traversal(node->right);
else
return;
}
public:
int getMinimumDifference(TreeNode *root) {
vec.clear();
traversal(root);
if (vec.size() < 2)
return 0;
int result = INT_MAX;
for (int i = 1; i < vec.size(); i++) { // 统计有序数组的最小差值
result = min(result, vec[i] - vec[i - 1]);
}
return result;
}
};
修改遍历逻辑即可
void traversal(TreeNode *root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // 将二叉搜索树转换为有序数组
traversal(root->right);
}
此外,我们还可以在遍历中进行计算,使用pre指针和cur指针
class Solution {
private:
int result = INT_MAX;
TreeNode* pre = NULL;
void traversal(TreeNode* cur) {
if (cur == NULL) return;
traversal(cur->left); // 左
if (pre != NULL){ // 中
result = min(result, cur->val - pre->val);
}
pre = cur; // 记录前一个
traversal(cur->right); // 右
}
public:
int getMinimumDifference(TreeNode* root) {
traversal(root);
return result;
}
};
迭代法
利用栈模拟递归
501.二叉搜索树中的众数
思路
题解
初见写出来的狗屎代码。这下知道用中序遍历了,但是关于最大频率的处理不对。
class Solution {
private:
std::vector<int> vec;
void traversal(TreeNode* root) {
if (root == nullptr) return;
traversal(root->left);
vec[root->val]++;
traversal(root->right);
}
public:
vector<int> findMode(TreeNode* root) {
traversal(root);
int idx = 0;
int cur = 0;
int value = 0;
std::vector<int> res;
for(auto it : vec) {
if (it > cur) {
cur = it;
value = idx;
}
idx++;
}
res.push_back(value);
return res;
}
};
用map遍历两次,应该算暴力解法
class Solution {
private:
unordered_map<int, int> map; // 统计频率
void traversal(TreeNode* root) {
if (root == nullptr) return;
traversal(root->left);
map[root->val]++; // 统计频率
traversal(root->right);
}
public:
vector<int> findMode(TreeNode* root) {
map.clear();
traversal(root);
vector<int> result;
int maxCount = 0;
// 第一次遍历找到最大频率
for (const auto& pair : map) {
maxCount = max(maxCount, pair.second);
}
// 第二次遍历找出所有出现次数等于maxCount的元素
for (const auto& pair : map) {
if (pair.second == maxCount) {
result.push_back(pair.first);
}
}
return result;
}
};
将map转换成vec进行排序
class Solution {
private:
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历
if (cur == NULL) return ;
map[cur->val]++; // 统计元素频率
searchBST(cur->left, map);
searchBST(cur->right, map);
return ;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
}
public:
vector<int> findMode(TreeNode* root) {
unordered_map<int, int> map; // key:元素,value:出现频率
vector<int> result;
if (root == NULL) return result;
searchBST(root, map);
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序
result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {
// 取最高的放到result数组中
if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
else break;
}
return result;
}
};
利用二叉搜索树的特性进行求解。因为中序遍历出来的元素是个有序数组,所以我们只需要比较相邻两个元素就可以得出出现频率了。
我们仍然需要使用pre指针和cur指针的技巧。
class Solution {
private:
int maxCount = 0; // 最大频率
int count = 0; // 统计频率
TreeNode* pre = NULL;
vector<int> result;
void searchBST(TreeNode* cur) {
if (cur == NULL) return ;
searchBST(cur->left); // 左
// 中
if (pre == NULL) { // 第一个节点
count = 1;
} else if (pre->val == cur->val) { // 与前一个节点数值相同
count++;
} else { // 与前一个节点数值不同
count = 1;
}
pre = cur; // 更新上一个节点
if (count == maxCount) { // 如果和最大值相同,放进result中
result.push_back(cur->val);
}
if (count > maxCount) { // 如果计数大于最大值频率
maxCount = count; // 更新最大频率
result.clear(); // 很关键的一步,不要忘记清空result,之前result里的元素都失效了
result.push_back(cur->val);
}
searchBST(cur->right); // 右
return ;
}
public:
vector<int> findMode(TreeNode* root) {
count = 0;
maxCount = 0;
pre = NULL; // 记录前一个节点
result.clear();
searchBST(root);
return result;
}
};
增强for循环中使用 const auto& 的原因:
-
性能考虑
&(引用)避免了对 map 中元素的拷贝- 直接引用原始数据,减少内存使用和复制开销
-
const 的作用
- 保证在遍历过程中不会修改 map 中的数据
- 增加代码安全性
- 明确表达"只读"意图
-
auto 的作用
- 自动推导类型,简化代码
- 实际类型是 pair<const int, int>
对比不同写法:
// 1. 不推荐: 会产生拷贝
for (auto pair : map) { ... }
// 2. 不推荐: 可能修改数据
for (auto& pair : map) { ... }
// 3. 推荐: 既高效又安全
for (const auto& pair : map) { ... }
这样写既保证了性能,又保证了数据安全性。
236.二叉树的最近公共祖先
思路
利用了前序遍历的回溯思想。
自底向上的寻找公共祖先。首先从遍历左子树开始,如果在左子树中的某一个节点中发现了指定节点p,就立马return此节点给其父节点,这样left就有了一个值,这时候我们就在刚刚找到的p节点的父节点处,此时我们寻找这个节点的右子树,看看是否能寻找到右节点,如果能找到的话,那这个节点就是我们要找的公关祖先,所以我们直接return这个节点到其父节点,在这个公共祖先的父节点中,我们找到的节点可能是左子树也可能是右子树,所以只需要左右子树一个有值,我们就返回那个不为null的值,这样就实现了传递的过程。
表述不太好,可以结合着代码和一下图片理解。
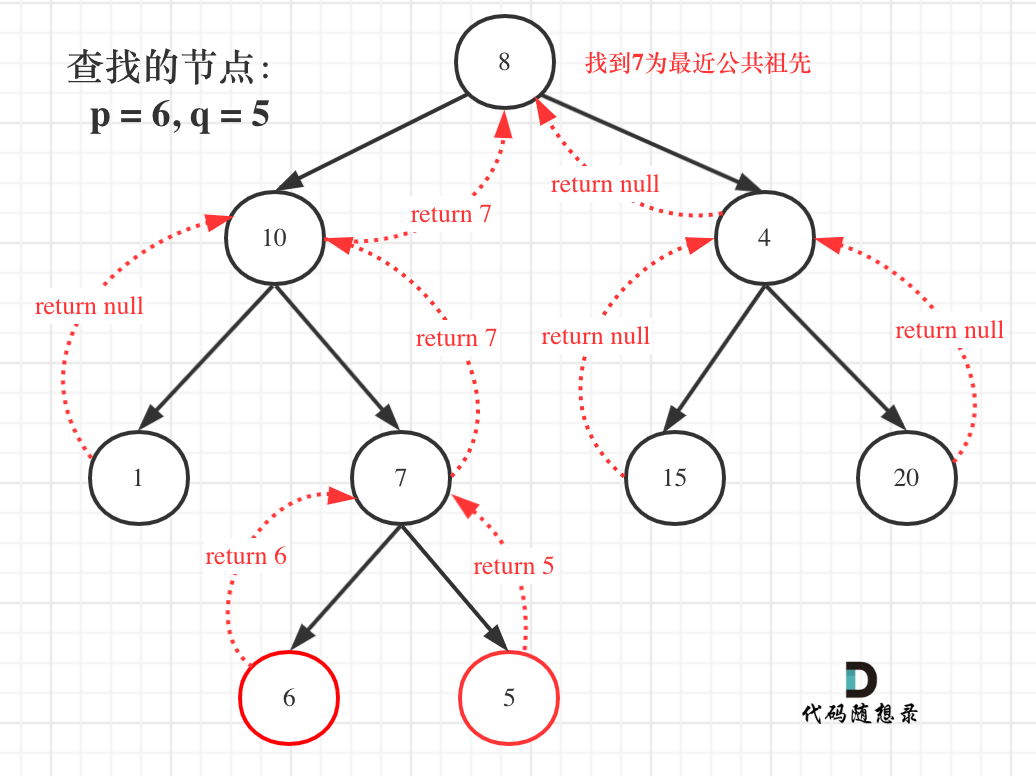
题解
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == q || root == p || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root;
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else { // (left == NULL && right == NULL)
return NULL;
}
}
};

https://shorturl.fm/O7GPt