本文最后更新于 411 天前,其中的信息可能已经有所发展或是发生改变。
110.平衡二叉树
题目描述:给定一颗二叉树,判断它是否是平衡二叉树。
递归法
后序遍历
本题适合采用后序遍历,先遍历完左右子树,从底部开始累加高度。
- 后序遍历
class Solution {
public:
int getHight(TreeNode *node) {
// 终止条件
if (!node) {
return 0;
}
// 计算左右子树高度
int left = getHight(node->left);
if (left == -1) {
return -1;
}
int right = getHight(node->right);
if (right == -1) {
return -1;
}
// 中,处理刚刚左右节点的父节点,也就是中
return abs(left - right) > 1 ? -1 : 1 + max(left, right);
}
bool isBalanced(TreeNode *root) {
return getHight(root) == -1 ? false : true;
}
};
257.二叉树的所有路径
题目描述:给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。
递归法
- 参数和返回类型:当前节点,当前路径,结果
- 终止条件:走到了叶子结点,处理收集到的节点
- 单层逻辑:先走当前节点左边的节点,收集结果,再回溯到当前节点,再收集结果
思路
先向下找到最深的一条路,然后返回(回溯)到上一级,走另一条路,如果没有另一条路也是直接再回溯到上一个节点。
关于回溯的理解
当一条路遍历到了最底层的时候,回溯到上一个节点,如果这时候path不是一个引用的话(见下方另一个版本),相当于直接回溯了一次,因为递归返回一次到达上一个stack frame的时候,path也应该回到上一个stack frame中的状态,但是下面的代码用的是引用,所以path相对于每一次递归而言并不是局部变量,所以递归返回的时候path并没有做回溯,所以需要手动的pop一次来达成回溯的目的。
- 直接体现回溯的代码(前序遍历)
class Solution {
private:
void traversal(TreeNode *node, vector<int>& path, vector<string>& res) {
path.push_back(node->val); // 中
//终止条件,以及处理收集到的节点的逻辑
if (node->left == NULL && node->right == NULL) {
string sPath;
for (int i = 0 ;i < path.size() - 1;i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
res.push_back(sPath);
return;
}
if (node->left) {
traversal(node->left, path, res);
path.pop_back();//回溯
}
if (node->right) {
traversal(node->right, path, res);
path.pop_back();//回溯
}
}
public:
vector<string> binaryTreePaths(TreeNode *root) {
vector<string> res;
vector<int> path;
traversal(root, path, res);
return res;
}
};
- 更加简洁的代码(前序遍历)
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // 中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result); // 左 回溯
if (cur->right) traversal(cur->right, path + "->", result); // 右 回溯
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
404.左叶子之和
题目描述:给定二叉树的根节点 root ,返回所有左叶子之和。
递归法
我自己的解法
思路
- 终止条件是当前节点没有左右节点
- 左子树按照以往的方式正常处理,而右子树需要判断右节点是否含有左右子树,如果有就处理,没有就不处理。
- 遍历方法:一种特殊的遍历
class Solution {
public:
void getLeft(TreeNode *node, vector<int> &res) {
// 终止条件
if (node->left == NULL && node->right == NULL) {
res.push_back(node->val);
return;
}
//左
if (node->left) {
getLeft(node->left, res);
}
//右
if (node->right && (node->right->left || node->right->right)) {
getLeft(node->right, res);
}
}
int sumOfLeftLeaves(TreeNode *root) {
int sum = 0;
vector<int> res;
if (!root->left && !root->right) {
return 0;
}
getLeft(root, res);
for (int i : res) {
sum += i;
}
return sum;
}
};
官方题解
思路
将右子树的处理逻辑和左子树统一化,处理左子树的时候,遍历到左右节点都为空的时候返回,将左节点的值拿到,回溯,然后遍历右子树,将右节点传入递归函数时,走的还是左子树的处理逻辑。总之要好好理解递归,当栈帧没有完全被释放的时候,return的值总会是传递到上一个栈帧中,比如说前一个的sum作为返回值传递到上一个的leftValue中,这一点要好好理解。
- 后序遍历
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0;
int leftValue = sumOfLeftLeaves(root->left); // 左
if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况
leftValue = root->left->val;
}
int rightValue = sumOfLeftLeaves(root->right); // 右
int sum = leftValue + rightValue; // 中
return sum;
}
};
222.完全二叉树的节点个数
题目描述:给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
按照普通二叉树来解题
思路
简单的遍历并累加
迭代法
使用层序遍历能很方便的得到答案,所以不赘述。
- 层序遍历
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
result++; // 记录节点数量
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};
递归法
- 后序遍历
class Solution {
private:
int getNodesNum(TreeNode* cur) {
if (cur == NULL) return 0;
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
}
public:
int countNodes(TreeNode* root) {
return getNodesNum(root);
}
};
利用完全二叉树特性
满二叉树节点数=2^h - 1
思路
将完全二叉树划分为几个满二叉树,利用公式计算
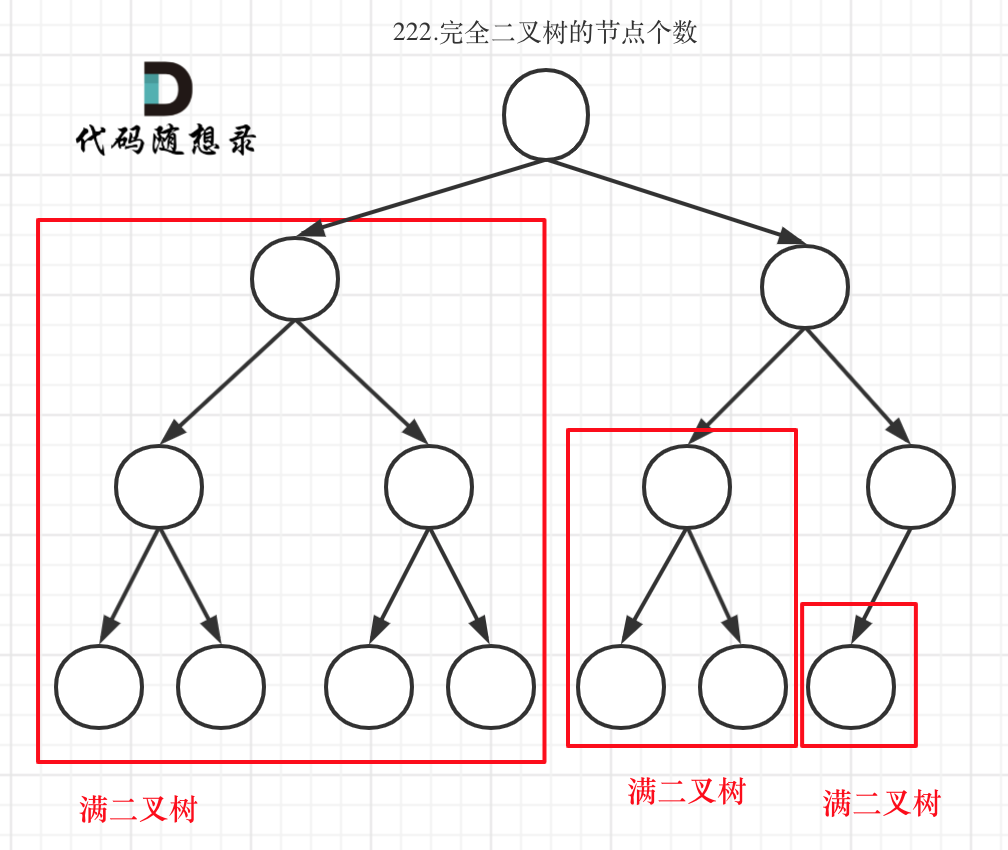
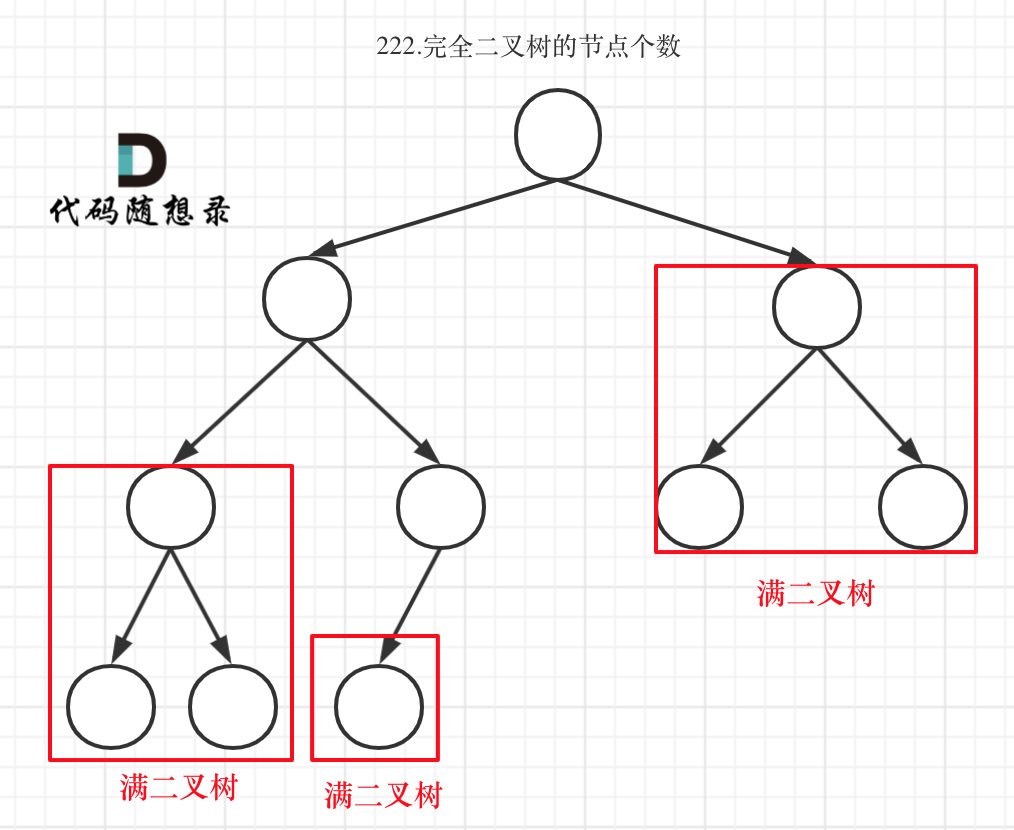
- 判断子树是否为满二叉树的逻辑
向左遍历深度等于向右遍历深度的时候,就说明为满二叉树
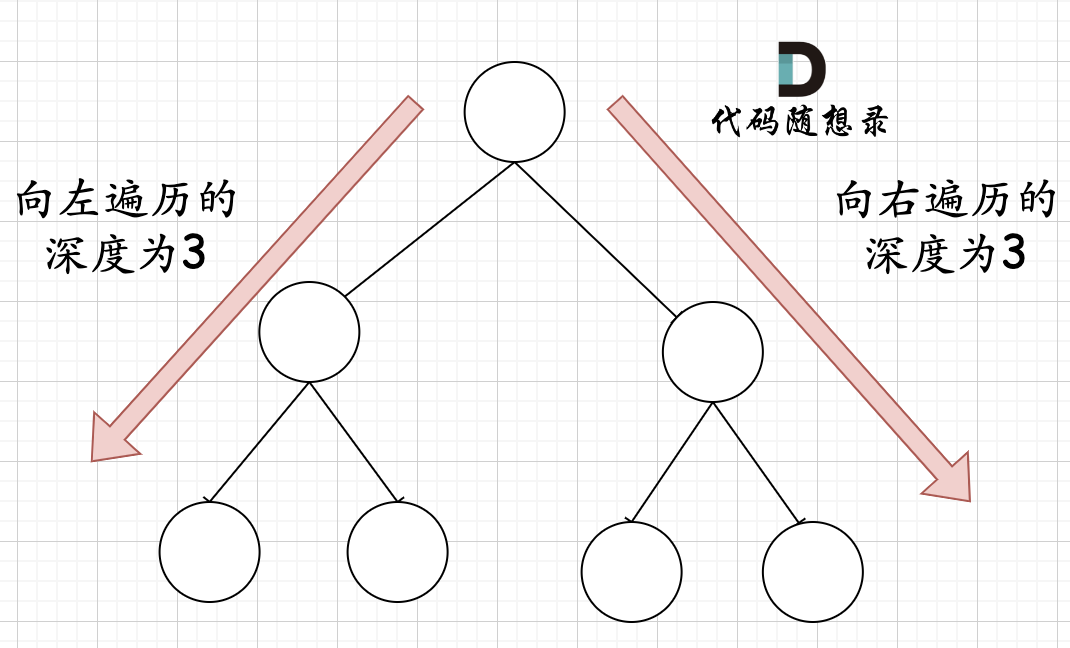
- 后序遍历
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
